What is Diffie-Hellman Key Exchange/Sharing/Establishment

Diffie-Hellman key agreement algorithm was developed by Dr. Whitfield Diffie and Dr. Martin Hellman in 1976, to establish shared secret keys in two different devices. The Diffie-Hellman key exchange is a wonderful mathematical algorithm, which allows two parties who have no prior knowledge to generate same secret keys. Diffie-Hellman key agreement algorithm is widely used in security protocols like Internet Protocol Security (IPSec), Secure Shell (SSH) and Transport Layer Security (TLS).

OmniSecuR1 and OmniSecuR2 are two routers, who want to securely generate secret keys.

OmniSecuR1 and OmniSecuR2 do not want to send the keys via insecure channel like internet, because the keys may be exposed to eavesdroppers or hackers. Diffie-Hellman mathematical algorithm suggests following steps to generate Encryption Key without sending the original secret Key via insecure channel like internet. Diffie-Hellman key agreement algorithm uses prime numbers to generate keys. A Prime Number is one which can be divided only by itself and by 1, without a remainder.

• OmniSecuR1 and OmniSecuR2 agree on a prime number "p" (prime modulus) and other number "g" (generator). In practical Diffie-Hellman, prime number "p" is a very large number.

• OmniSecuR1 chooses a secret number "a", and sends OmniSecuR2 (g^a) MOD p = A. OmniSecuR1 will never reveal its secret number "a" to anyone.

• OmniSecuR2 chooses a secret number "b", and sends OmniSecuR1 (g^b) MOD p = B. OmniSecuR2 will never reveal its secret number "b" to anyone.

• OmniSecuR1 computes Key1 = (B^a ) MOD p

• OmniSecuR2 computes Key2 = (A^b ) MOD p

The Key generated Key1 and Key2 are same on both Routers (Key1=Key2).

Diffie-Hellman explained with an example

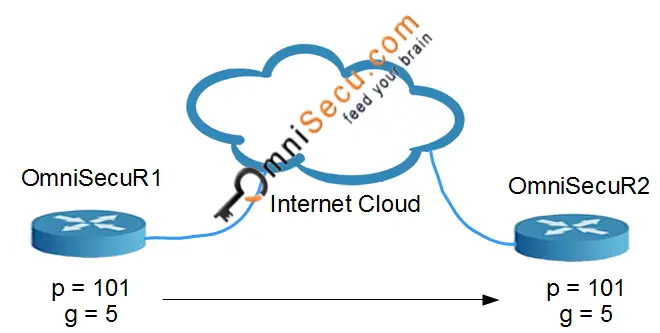
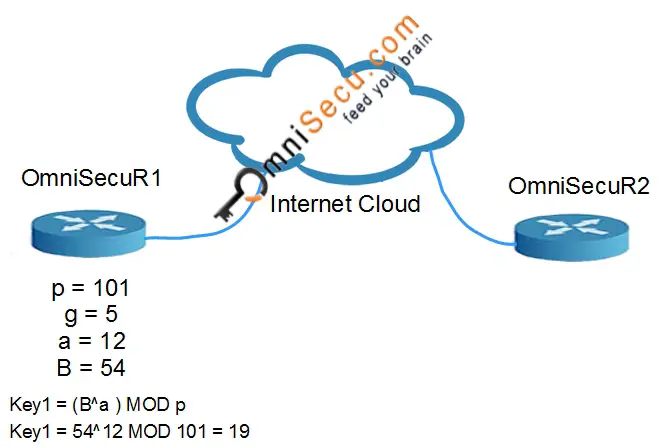
• Both OmniSecuR1 and OmniSecuR2 agree values "p" and "g" as p=101 and g=5.

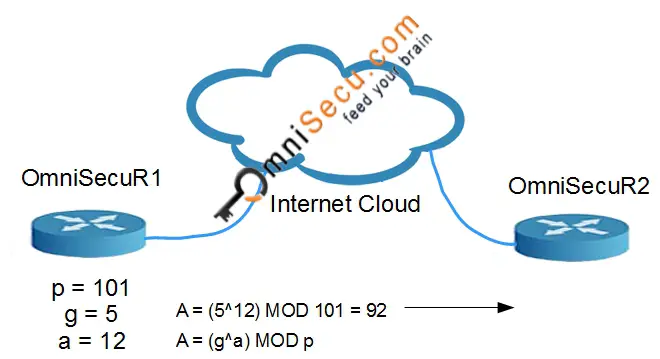
• OmniSecuR1 chooses the secret number "a" as 12. OmniSecuR1 computes and sends A to OmniSecuR2. In this case, A = (5^12) MOD 101 = 92

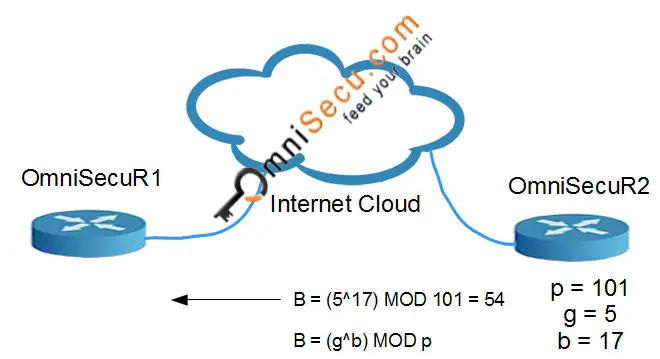
• OmniSecuR2 chooses the secret number "b" as 17. OmniSecuR2 computes and sends B to OmniSecuR1. In this case, B = (5^17) MOD 101 = 54

• OmniSecuR1 computes Key1 = (B^a ) MOD p. In this case, Key1 = 54^12 MOD 101 = 19

• OmniSecuR2 computes Key2 = (A^b ) MOD p. In this case, Key2 = 92^17 MOD 101 = 19

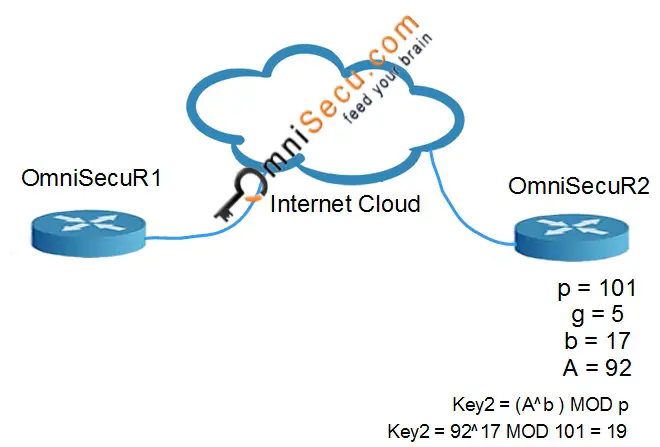
Now, you can observe that Key1 = Key2 = 19. The values Key1/Key2 are never exchanged over internet. The values "p" and "g" can be shared over internet and no protection is required for values "p" and "g". In real-time, much larger values of a, b, and p are required for Diffie-Hellman Key establishment.